Luvun juurtaminen harpilla ja viivoittimella

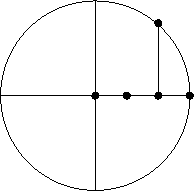
Tunnetusti harpilla ja viivoittimella voidaan konstruoida vain niitä pisteitä, joiden koordinaatit on ilmaistavissa aiemmin tunnettujen pisteiden koordinaattien lineaarikuvausten ja neliöjuurten avulla. Toisaalta vastaavasti voidaan mikä tahansa tällainen neliöjuurilauseke konstruoida harpilla ja viikoittimella. Lähdetään liikkeelle origokeskeisestä r-säteisestä ympyrästä $x^2+y^2=r^2$ ja x-akselin pisteestä $(x_0,0)$ , missä $x_0\in(0,r)$ . Tällöin piste $y_0=\sqrt{r^2-x_0^2}$ ilmeisesti sijaitsee ympyrän kehällä. Toisaalta, koska $r^2-x_0^2=(r-x_0)(r+x_0)$ , voidaan mielivaltaisen luvun neliöjuuri tai mielivaltaisen kahden luvun geometrinen keskiarvo laskea ratkaisemalla yhtälöpari
$\left\{\begin{array}{ccc}r-x_0=m\\r+x_0=n\end{array}\right. ,$
jolloin saadaan $r=\frac{n+m}{2},\quad x_0=\frac{n-m}{2}$ . Nyt siis esimerkiksi $\sqrt{5}$ voitaisiin laskea asettamalla $m=1,\ n=5$ , jolloin $r=3,\ x_0=2$ ja $\sqrt{5}$ siis sen viivan pituus, joka saadaan mittaamalla suora viiva pisteestä $(2,0)$ ylöspäin 3-säteiselle ympyrälle.